Performance of Sorting or Searching in C programming language

Performance of Sorting or Searching

One of the chief concerns in searching and sorting is speed. Often, this concern is misguided, because the
sort or search takes negligible time compared to the rest of the program. For most sorting and searching
applications, you should use the easiest method available (see FAQs III.1 and III.4). If you later find that the
program is too slow because of the searching or sorting algorithm used, you can substitute another method
easily. By starting with a simple method, you haven’t invested much time and effort on code that has to be
replaced.

One measure of the speed of a sorting or searching algorithm is the number of operations that must be
performed in the best, average, and worst cases (sometimes called the algorithm’s complexity). This is
described by a mathematical expression based on the number of elements in the data set to be sorted or
searched. This expression shows how fast the execution time of the algorithm grows as the number of
elements increases. It does not tell how fast the algorithm is for a given size data set, because that rate depends on the exact implementation and hardware used to run the program.

The fastest algorithm is one whose complexity is O(1) (which is read as “order 1”). This means that the
number of operations is not related to the number of elements in the data set. Another common complexity
for algorithms is O(N) (N is commonly used to refer to the number of elements in the data set). This means
that the number of operations is directly related to the number of elements in the data set. An algorithm with
complexity O(log N) is somewhere between the two in speed. The O(log N) means that the number of
operations is related to the logarithm of the number of elements in the data set.

 -------------------------------------------------------------------------------------------------------------

NOTE : If you’re unfamiliar with the term, you can think of a log N as the number of digits needed to write
the number N. Thus, the log 34 is 2, and the log 900 is 3 (actually, log 10 is 2 and log 100 is 3—
log 34 is a number between 2 and 3).

If you’re still with me, I’ll add another concept. A logarithm has a particular base. The logarithms
described in the preceding paragraph are base 10 logarithms (written as log10 N), meaning that
if N gets 10 times as big, log N gets bigger by 1. The base can be any number. If you are comparing
two algorithms, both of which have complexity O(log N), the one with the larger base would be
faster. No matter what the base is, log N is always a smaller number than N.

---------------------------------------------------------------------------------------------------------------
An algorithm with complexity O(N log N) (N times log N ) is slower than one of complexity O(N), and an
algorithm of complexity O(N2) is slower still. So why don’t they just come up with one algorithm with the
lowest complexity number and use only that one? Because the complexity number only describes how the
program will slow down as N gets larger.

The complexity does not indicate which algorithm is faster for any particular value of N. That depends on
many factors, including the type of data in the set, the language the algorithm is written in, and the machine
and compiler used. What the complexity number does communicate is that as N gets bigger, there will be
a point at which an algorithm with a lower order complexity will be faster than one of a higher order
complexity.

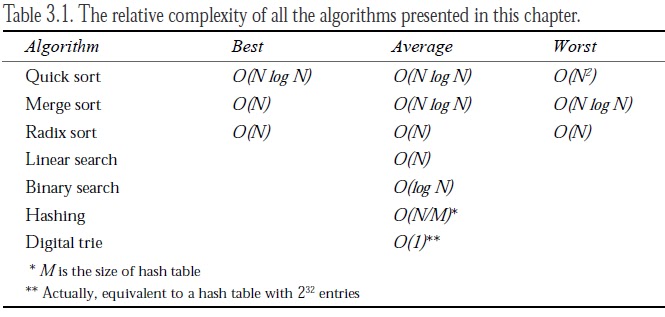
Table 3.1 shows the complexity of all the algorithms listed in this chapter. The best and worst cases are given
for the sorting routines. Depending on the original order of the data, the performance of these algorithms
will vary between best and worst case. The average case is for randomly ordered data. The average case
complexity for searching algorithms is given. The best case for all searching algorithms (which is if the data
happens to be in the first place searched) is obviously O(1). The worst case (which is if the data being searching

for doesn’t exist) is generally the same as the average case.

To illustrate the difference between the complexity of an algorithm and its actual running time, Table 3.2
shows execution time for all the sample programs listed in this chapter. Each program was compiled with
the GNU C Compiler (gcc) Version 2.6.0 under the Linux operating system on a 90 MHz Pentium
computer. Different computer systems should provide execution times that are proportional to these times.

-------------------------------------------------------------------------------------------------------------

NOTE : All times are in seconds. Times are normalized, by counting only the time for the program to
perform the sort or search.
The 2000–10000 columns indicate the number of elements in the data set to be sorted or searched.
Data elements were words chosen at random from the file /usr/man/man1/gcc.1 (documentation
for the GNU C compiler).
For the search algorithms, the data searched for were words chosen at random from the file /usr/
man/man1/g++.1 (documentation for the GNU C++ compiler).
qsort() and bsearch() are standard library implementations of quick sort and binary search,
respectively. The rest of the programs are developed from scratch in this chapter.

-----------------------------------------------------------------------------------------------------------
 

This information should give you a taste of what issues are involved in deciding which algorithm is
appropriate for sorting and searching in different situations. The book The Art of Computer Programming,
Volume 3, Sorting and Searching, by Donald E. Knuth, is entirely devoted to algorithms for sorting and
searching, with much more information on complexity and complexity theory as well as many more
algorithms than are described here.